Excel PMT Function Mastery: A Comprehensive Guide to Financial Planning

Examples of the Excel PMT Function

Here are few examples demonstrating the usage of the Excel PMT function:

Example 1: Calculating Loan Payments

Suppose you have a loan of $10,000 with an annual interest rate of 7%, and you plan to repay it over 3 years (considering a constant interest rate and a fixed period). In cell B6, input the following formula to calculate the monthly payment:

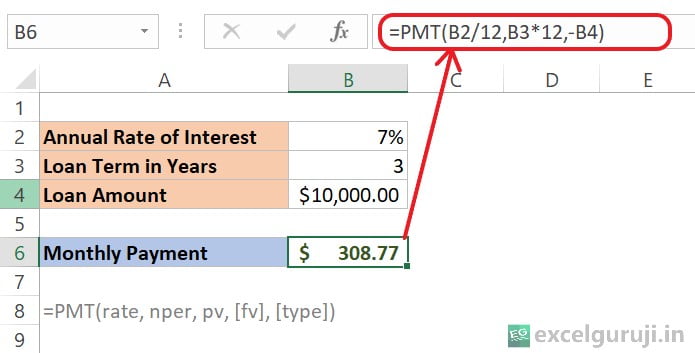
Let’s break down the formula: =PMT(B2/12,B3*12,-B4)

• B2/12: The annual interest rate is in cell B2, which is 7%. To get the monthly interest rate, we divide this by 12 (the number of months in a year). So, B2/12 becomes 7%/12 or 0.0058333 (approximately).
• B3*12: The loan term is in years, and it is given in cell B3 as 3 years. To get the total number of monthly payments, we multiply this by 12. So, B3*12 becomes 36.
• –B4: The loan amount is in cell B4, which is $10,000.00. This value is usually negative in the PMT function to represent an outgoing payment.

When you calculate this, it results in approximately $ 308.77.

Tip: To calculate the overall amount paid throughout the loan term, simply multiply the PMT value obtained by the total number of payment periods (nper).

Example 2: Investment Planning

If you aim to save $50,000 for a future project and expect an annual return of 8% over 5 years, you can calculate the monthly savings required using the Excel PMT function. In cell B6, input the following formula:

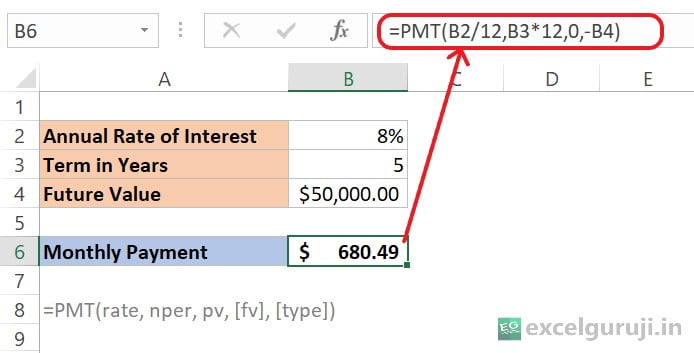
Let’s break down the formula: =PMT(B2/12,B3*12,0,-B4)

• B2/12: The annual interest rate is in cell B2, which is 8%. To get the monthly interest rate, we divide this by 12 (the number of months in a year). So, B2/12 becomes 8%/12 or approximately 0.0066667.
• B3*12: The term is in years, and it is given in cell B3 as 5 years. To get the total number of monthly payments, we multiply this by 12. So, B3*12 becomes 60.
• 0: This represents the present value, set to 0 in this scenario because you are starting with no initial savings (present value).
• -B4: The future value in cell B4 is $50,000. Although it is considered an incoming payment at the end of the term, by using a negative sign before the cell address, it signifies an outflow of funds from your pocket over a period of 5 years.

When you calculate this, it should indeed result in approximately $680.49. This positive value indicates the monthly savings required to reach a future value of $50,000 over a 5-year period at an 8% annual interest rate.

Note: Here, we use [FV] 4^thargument instead of PV 3^rd argument, because when saving for a goal, you might set [FV] as the target amount you want to achieve. PMT would then represent the regular savings or investment amount needed to reach that future value. On the other hand, PV might represent an initial investment or loan amount. The choice between using PV or FV depends on the specific financial scenario you are modeling or calculating.

Example 3: Handling Optional Argument

We used the [fv] (4^th argument) in the example 2; now, let’s explore how the investment varies by incorporating the [type] (5^th argument).

In this example, we will utilize the same parameters as in Example 2.

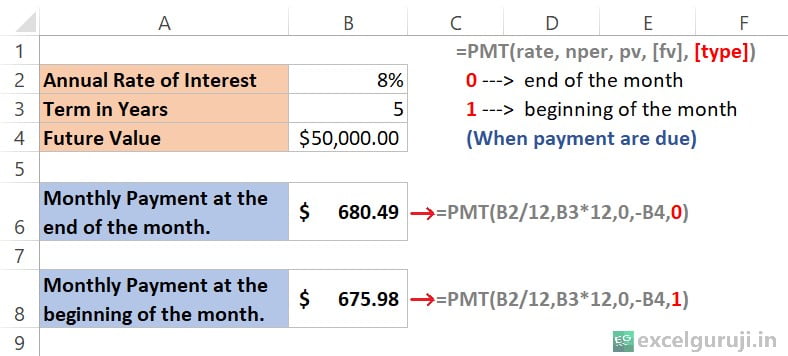
In the above example, we introduce the [type] parameter, the 5th argument in the PMT function, which allows us to specify when payments are made – either at the beginning or the end of the month.

• =PMT(B2/12, B3*12, 0, -B4, 0)
  • The [type] parameter is set to 0, indicating payments are made at the end of the month. If you omit the [type] parameter, the function defaults to 0. This means that, by default, payments are considered to occur at the end of each month.

• =PMT(B2/12, B3*12, 0, -B4, 1)
  • The [type] parameter is set to 1, indicating payments are made at the beginning of the month.

Extra Notes

● If the interest rate is less than or equal to -1 or the number of payment periods is 0, you will see a #NUM! error.

● When any of the given values are not numbers, you will get a #VALUE! error.

● When figuring out monthly or quarterly payments, make sure to change annual interest rates or the number of periods into months or quarters.

● To know the total paid over the loan time, just multiply the PMT amount by the number of payments (nper).

● The Excel PMT function gives you the loan amount and interest but doesn’t include extra costs like fees, taxes, or reserve payments.

● If the PMT result is way higher or lower than expected, double-check that you are using the right units for interest rate and number of periods. Make sure to convert annual rates to monthly or quarterly rates, and years to weeks, months, or quarters, as shown in previous examples.